問題
夏祭りも佳境に入り、子どもたちがそろそろ宝探しゲームを始めるところです。
宝探しをする場所はとても広く、二つのとても大きな崖が平行に走っています。
崖と垂直に$y$軸を取ると、二つの崖はそれぞれ$A\leqq y\leqq B, C\leqq y\leqq D$の領域全体にあり、高低差もあるので子どもたちだけでは渡ることができません。
今、$N$人の子どもは全員$y\lt A$の領域にいて、$i$番目の子どもは点$(p_i,q_i)$にいます。
子どもはそれぞれ自分の目標とする宝の座標を持っていて、$i$番目の子どもの宝の座標は$(r_i, s_i)$です。
全ての宝は$y\gt D$の領域にあります。
しかし、宝探し開催直前になって、スタッフたちは崖に橋を架けていないことに気がつきました。
橋はすでに崖の大きさに合わせたものが作ってあるのですが、まだ崖に設置されていません。
例年なら子どもが疲れないような橋の位置をゆっくりと検討するのですが、そのような時間はもうありません。
そこで、夏祭りに参加していたあなたに白羽の矢が立ちました。
全ての子どもの座標とその子供が目指す宝の座標が与えられるので、全ての子どもがそれぞれの宝に到達するまでの総移動距離の和が最小になるような橋のかけ方を求めてください。
ただし、危険なので橋は$y$軸に平行に架けなければいけません。また、橋の幅は極めて小さいものとします。
入力
$N\ A\ B\ C\ D$ $p_1\ q_1\ r_1\ s_1$ $p_2\ q_2\ r_2\ s_2$ : $p_N\ q_N\ r_N\ s_N$
1行目には子どもの数$N$($1\leqq N\leqq10000$)と2つの崖の位置を示す整数$A,B,C,D$($0 \lt A \lt B \lt C \lt D \lt 10000$)が与えられます。
つづく$N$行のうち$i$行目には、4つの整数$p_i,q_i,r_i,s_i$($0\leqq p_i,q_i,r_i,s_i\leqq10000,q_i \lt A,D \lt s_i$)が与えられます。これは$i$人目の子どもが$(p_i,q_i)$にいて、宝の座標が$(r_i,s_i)$であることを示しています。
出力
子どもたちの総移動距離の和が最小になるように橋を架けるときの二つの橋が架けられる$x$座標を、$A\leqq y\leqq B$に架けた橋と$C\leqq y\leqq D$に架けた橋について順番に空白を区切りとして一行に出力しなさい。
この問題は許容誤差が設定されている。
出力値と想定解の絶対誤差または相対誤差が$10^{-5}$未満のテストケースは正答とみなす。
入出力例
入力例1
2 25 35 65 75 4 4 4 96 96 4 96 96
出力例1
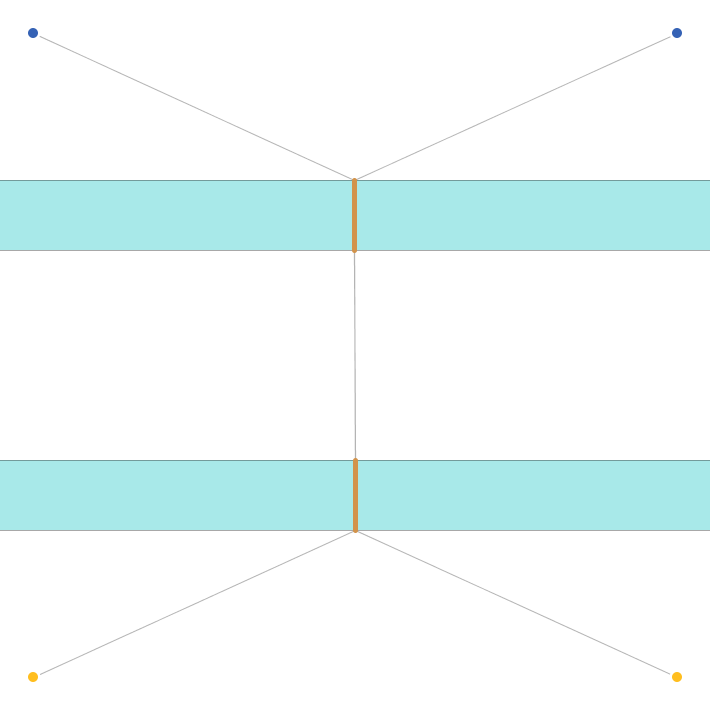
50.0000000000 50.00000000000子どもを青い点、宝を黄色い点とすると、図のようになります。橋を二人の子供の中央に架けるのが最適です。
入力例2
3 25 35 65 75 11 4 78 87 97 11 78 88 17 12 78 89
出力例2
63.3601658117 73.5843102673
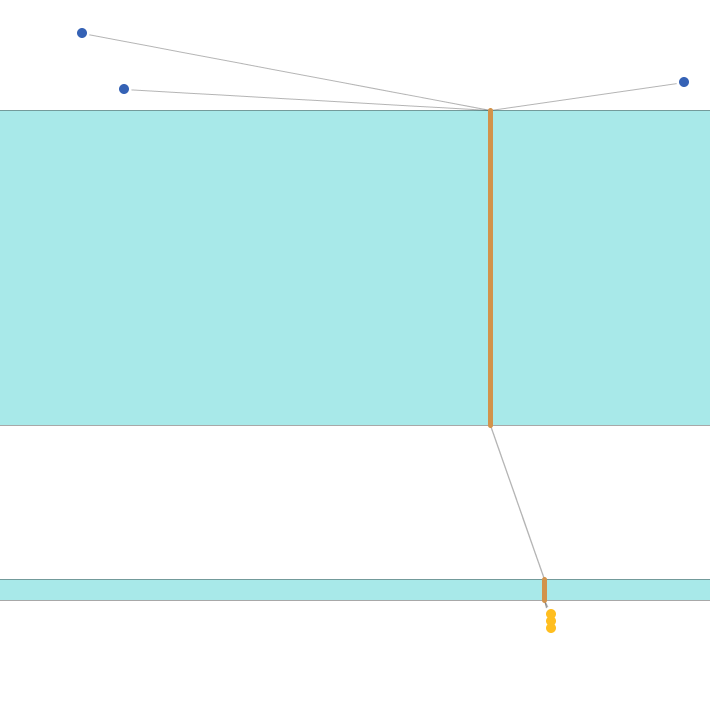
二つの崖の幅は等しいとは限りません。
入力例3
36 30 40 50 60 19 3 39 73 32 3 44 73 42 3 47 73 54 3 51 73 32 5 59 73 19 6 67 73 32 6 79 73 19 7 79 74 32 7 39 75 54 7 79 75 32 8 67 77 42 9 59 78 42 10 67 80 19 11 39 81 32 11 59 81 54 11 39 83 19 13 46 83 42 13 49 83 46 13 51 83 49 13 67 83 51 13 70 83 54 13 74 83 32 14 76 83 54 14 79 83 19 16 59 84 32 17 51 85 54 17 59 87 19 19 79 87 32 20 51 89 19 21 79 90 54 21 79 92 19 23 39 94 54 23 48 94 19 24 51 94 32 24 59 94 54 24 79 94
出力例3
46.3260267897 49.4837810349
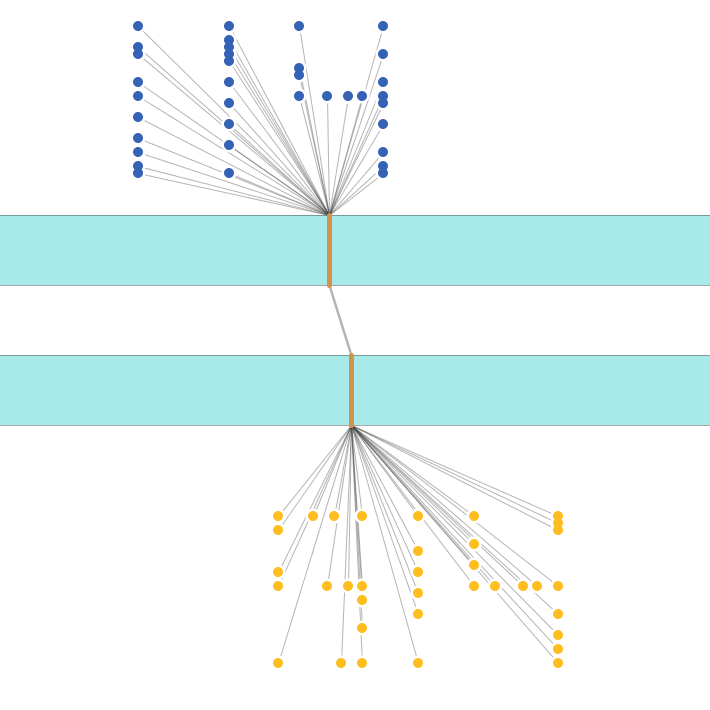
渡って、どうぞ