問題
P君とQ君は陣取りゲームを行っている。P君が先行である。
このゲームでは、$H×W$の盤面が$1×1$のマス目で区切られている。$i$行目、$j$列目のマス目をマス$(i,j)$と表記すると、マス$(i,j)$には整数$a_{ij}$が書かれている。
また、二つのボタンが盤面上に設置されている。1つ目のボタンはマス$(A,B)$に、2つ目のボタンはマス$(C,D)$に存在する。 二つのボタンの位置は互いに異なる。
ボタンの上にも(マス目上の数字とは別に)「カウンタ」と呼ばれる数字が書かれている。最初各ボタンのカウンタは0である。
二人は交互にいずれかのボタンを選んで押す。ボタンを押したあと、二人は陣地を以下のように獲得する。
①ボタンのカウンタの数字を$Q$とし、ボタンの位置をマス$(h,w)$としたとき、$abs(i-h)+abs(j-w)=Q$を満たす
すべての整数$i,j(1≦i≦H,1≦j≦W)$について、マス$(i,j)$がまだどちらの陣地にもなっていない場合、自分の陣地にする。
②カウンタの数字を1増やす
(ただし、$abs(x)$とは$x$の絶対値であり、$x$が正の場合は$x$、そうでない場合は$-x$である。)
参考までに①の条件を以下に具体例をもって図示する。例えば、$Q=4$,$h=6$,$w=7$でボタンを押した場合、緑の正方形の位置がマス$(i,j)$の要件を満たすことになる。
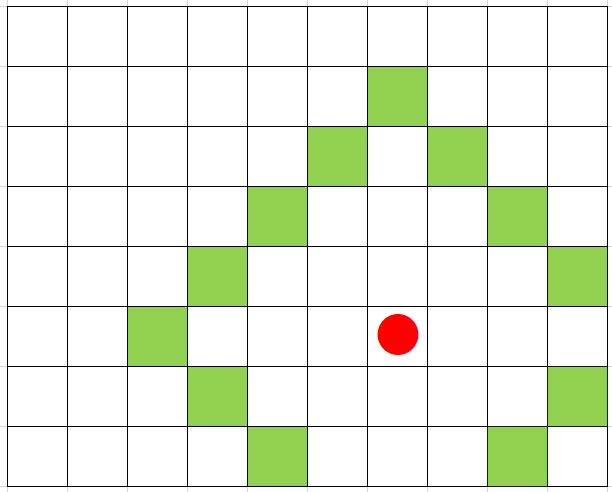
すべての陣地が自分か相手のものになった時点でゲームは終了する。得点は自分の陣地になったマス目に書かれている整数の和である。
二人とも自分の最終的な得点を最大化するために最適な行動をとる。この時、P君は最終的に何点獲得するだろうか?
14:12修正:表現を変更
入力
入力は標準入力で以下のように与えられる。
$H$ $W$
$A$ $B$ $C$ $D$
$a_{11}$ $a_{12}$ ... $a_{1W}$
$a_{21}$ $a_{22}$ ... $a_{2W}$
:
$a_{H1}$ $a_{H2}$ ... $a_{HW}$
出力
標準出力に、「P君が最終的に獲得する点数」を一行で出力せよ。末尾に必ず改行を入れること。
制約
すべての入力について、以下の制約を満たす。
・$1 \le H,W \le 1000$・$-10^9 \le a_{ij} \le 10^9$
・$1 \le A,C \le H,1 \le B,D \le W$
・$(A,B) \ne (C,D)$
この問題には部分点が設定されている。以下の小課題について正解した場合、対応する部分点が与えられる。
小課題1(+20点)
・$1 \le H,W \le 5$小課題2(+20点)
・$1 \le H,W \le 50$小課題3(+20点)
・$1 \le H,W \le 200$入出力例
入力例1
2 2 1 1 2 2 1 2 3 4
出力例1
5
解説
P君はまず1手目で左上のボタンか右下のボタンを押すことができる。どちらの場合でも、次のターンで相手に右上と左下の2+3=5を取られるので、次の手でもう片方の1マスを取ることになる。
いずれにせよ、P君は1+4=5点獲得する。これ以上良い点数は得られないので、答えは5である。
入力例2
2 2 1 1 2 2 100 -100 -100 100
出力例2
-100
解説
負の数が書かれたマスも存在することに注意せよ。
入力例3
4 5 2 2 3 4 1 -4 2 -6 5 2 -3 1 -9 1 2 -3 4 -5 6 8 -1 7 -1 0
出力例3
6