問題
P君の国には$N$個の町が存在している。各町は$1$から$N$までの整数が割り振られている。
また、人の歩く道が$M$本存在し、$i$本目の歩道は町$u_i$と町$v_i$を徒歩$t_i$分で行き来できることが知られている。
P君は鉄道を町$A$から町$B$に敷きたいと思った。P君の国の土地はとても険しいため開拓は難しく、既に存在する歩道に沿って鉄道を敷こうと考えた。
具体的には、まずP君は町$A$から町$B$まで、いくつかの歩道をたどって歩く経路のうち最も移動するのに必要な時間が短いものに沿って鉄道を敷こうとした。
次に、町$A,B$も含め、鉄道を敷く経路が通る各町に駅を設置しようとした。
そこで、P君は、すべての町についての「その町から最寄りの駅までにたどり着く最短時間」の総和を知りたくなった。
入力
入力は標準入力で以下のように与えられる。
$N$ $M$ $A$ $B$ $u_1$ $v_1$ $t_1$ $u_2$ $v_2$ $t_2$ : $u_M$ $v_M$ $t_M$
13:16訂正:誤った文章を修正
出力
標準出力に、「最寄りの駅までにたどり着く最短時間の総和」を一行で出力せよ。末尾に必ず改行を入れること。
制約
すべての入力について、以下の制約を満たす。
・$1 \le N \le 10^5$・$1 \le M \le 2 \times 10^5$
・$1 \le A,B \le N$ $(A \ne B)$
・$1 \le u_i,v_i \le N,$ $1 \le t_i \le 10^9$ $(1 \le i \le M)$
・すべての町は連結
・町$A$と町$B$を結ぶ最短路はただ一通り存在する
この問題には部分点が設定されている。以下の小課題について正解した場合、対応する部分点が与えられる。
小課題1(+20点)
・$1 \le N \le 1000$・$1 \le M \le 2000$
入出力例
入力例1
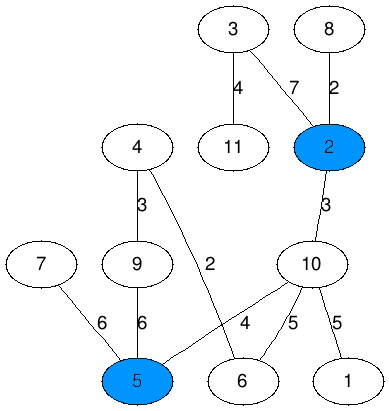
6 8 1 5 1 3 3 1 5 5 1 6 2 2 5 9 2 6 10 3 4 3 3 5 8 5 6 4
出力例1
20
解説
P君は町1と町5を結ぶ長さ5のパスに鉄道を引くので、駅を町1と町5に設置することになる。町1,3,4,6は町1の駅が最寄り駅であり、町2,5は町5の駅が最寄り駅である。よって答えは0+9+3+6+0+2=20である。
13:20訂正:誤った文章を修正
入力例2
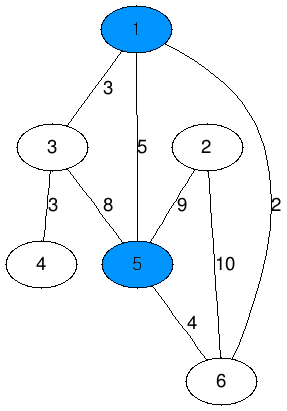
11 11 2 5 10 1 5 7 5 6 2 10 3 3 2 7 8 2 2 10 6 5 10 5 4 9 5 6 4 6 2 3 11 4 4 9 3
出力例2
49