問題
P君は家族でピクニックを楽しみに草原へやってきた。
草原は南北に$H$メートル、東西に$W$メートルの長方形であり、1×1メートルのマス目に区切られている。
各マス目の土地は草でおおわれているか、禿地かのいずれかである。
具体的には、草原の一番北西にあるマス目から南に$i-1$メートル、東に$j-1$メートル進んだマス目は、$a_{ij}$が1の場合草でおおわれており、0の場合禿地である。
今からP君は4つのマス目にぴったり重なるように、縦2メートル横2メートルの正方形のランチマットを敷く。
ただ、座る場所によって差が出ると不公平なので、P君は重なっている4つのマス目のすべてが草でおおわれているか、またはすべて禿地である必要があると考えた。
不公平の無いようにランチマットを敷く位置は何通りあるだろうか?
入力
入力は以下のように標準入力で与えられる。
$H$ $W$
$a_{11}$ $a_{12}$ ... $a_{1W}$
$a_{21}$ $a_{22}$ ... $a_{2W}$
:
$a_{H1}$ $a_{H2}$ ... $a_{HW}$
出力
ランチマットを敷く位置の通り数を一行で出力せよ。末尾に改行を入れること。制約
すべてのテストケースは以下の制約を満たす。・$2 \le H,W \le 1000$
・$a_{ij}$は0か1($1 \le i \le H$,$1 \le j \le W$)
入力例
入力例1
5 5 1 1 0 0 1 1 1 0 0 1 0 0 0 1 1 0 0 0 1 1 1 1 1 1 1
出力例1
6
解説
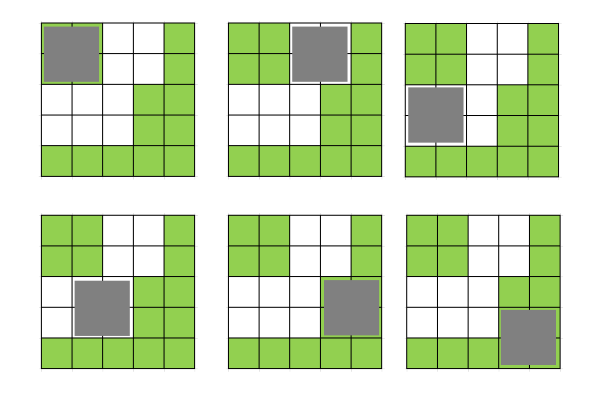
以下の図のように、ランチマットを敷く位置は6通り存在する
入力例2
6 6 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
出力例2
25