ストーリー※読まなくてもよい
某有名動画配信者のHちゃんは勉強と甘いものが苦手である。そのため、課題に頭を悩ませていた。その課題とは、線分が垂直に交わっているか判定するものである。Hちゃんはその判断すら危うい。
しかもこの課題は、線分の情報として、その端点しか与えられないのである。しぇんしぇーであるあなたは「ふにー…」となっているHちゃんを見かねて、この課題を解くプログラムを作ることにした。
問題
線分の端点 p(px,py) , q(qx,qy) が n 本分与えられる。
その中で、他の線分と垂直に交わっている線分の本数を表示し、その後番号を列挙せよ。
入力
n px1 py1 qx1 qy1 px2 py2 qx2 qy2 px3 py3 qx3 qy3 ・・・ pxn pyn qxn qyn
1 行目に線分の本数 n が与えられる。
2 行目から n + 1 行目にかけて 4 つの整数 px, py, qx, qy が与えられる。これらの座標が示す点 p( pxi , pyi ) , q( qxi ,qyi ) が線分の端点であることを表している。
出力
1 行目に他の線分と垂直に交わっている線分の本数を出力せよ。
2 行目に他の線分と垂直に交わっている線分の番号を昇順で出力せよ。最後の改行も忘れないようにすること(改行の前には空白は存在しない)。
他の線分と垂直に交わっている線分がない場合は"Nothing"と1行に表示せよ。
制約
全ての入出力ケースにおいて次の制約を満たす。
- 1 ≦ n ≦ 200
- 0 ≦ pxi , pyi , qxi , qyi ≦ 2000
また、全ての p , q において、両点が同じ座標であり、線分が作られないことはないものとする。
入出力例
入力例1
3 0 0 6 0 1 0 1 4 1 0 4 3
出力例1
2 1 2
入力例2
4 0 6 3 0 3 2 5 4 1 3 4 5 4 7 1 1
出力例2
Nothing
入力例3
5 2 0 0 6 1 3 4 4 5 2 2 2 1 2 4 1 3 6 0 5
出力例3
3 1 2 5
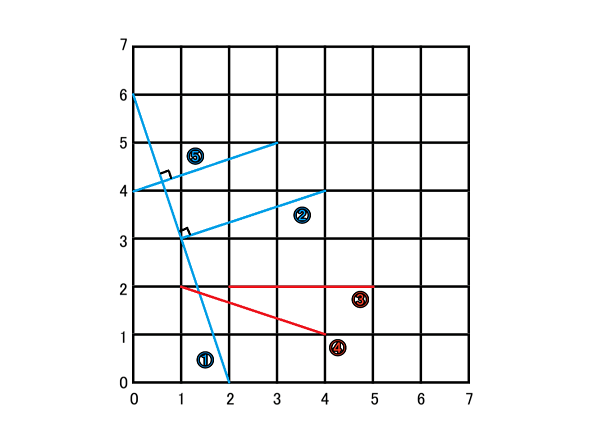
入出力例3の図は以下のようになる。
追記
問題の不備を発見した場合はei1623まで報告をお願いします。
履歴
2018/02/05 18:00頃にテストケースの不備を修正するため、テストケースの更新およびリジャッジをしました。
2018/02/05 18:18頃にテストケースの更新およびリジャッジをしました。