問題
ei1710はxy平面上に迷い込んだ。
この平面には縦にh本,横にw本の道が等間隔に通っている。
道の交点、つまり角にはお金が落ちているかもしれない。
せっかくなのでei1710は落ちているお金をできるだけたくさん拾いながら最短でこの平面から抜け出したい。
ei1710が迷い込んだ平面の地図が与えられるので、お金は最大でいくら拾えるか計算してほしい。
なお、ei1710は最初に座標(0, 0)におり、座標(h - 1, w - 1)に辿りつくと平面から脱出できる。
当然、座標(h - 1, w - 1)に落ちているお金も拾っていく。彼は強欲なのだ。
入力
h w a0, 0 a0, 1 ... a0, w - 1 a1, 0 a1, 1 ... a1, w - 1 ... ... ah - 1, 0 ah - 1, 1 ... ah - 1, w - 1
最初に、平面の高さと幅が与えられる。
その後、h行w列にわたって平面の情報が与えられる。
ai, jは角(i, j)に落ちているお金をあらわす。
出力
ei1710が拾える金額の最大値を1行に出力せよ。
制約
全ての入出力ケースにおいて以下を満たす。
- 1 ≦ h , w ≦ 1000
- 0 ≦ a i, j ≦ 10000 (0 ≦ i ≦ h -1, 0 ≦ j ≦ w - 1)
入出力例
入力1
4 5 0 0 0 500 800 800 0 0 0 0 0 300 0 0 0 0 0 0 0 0
出力1
1300
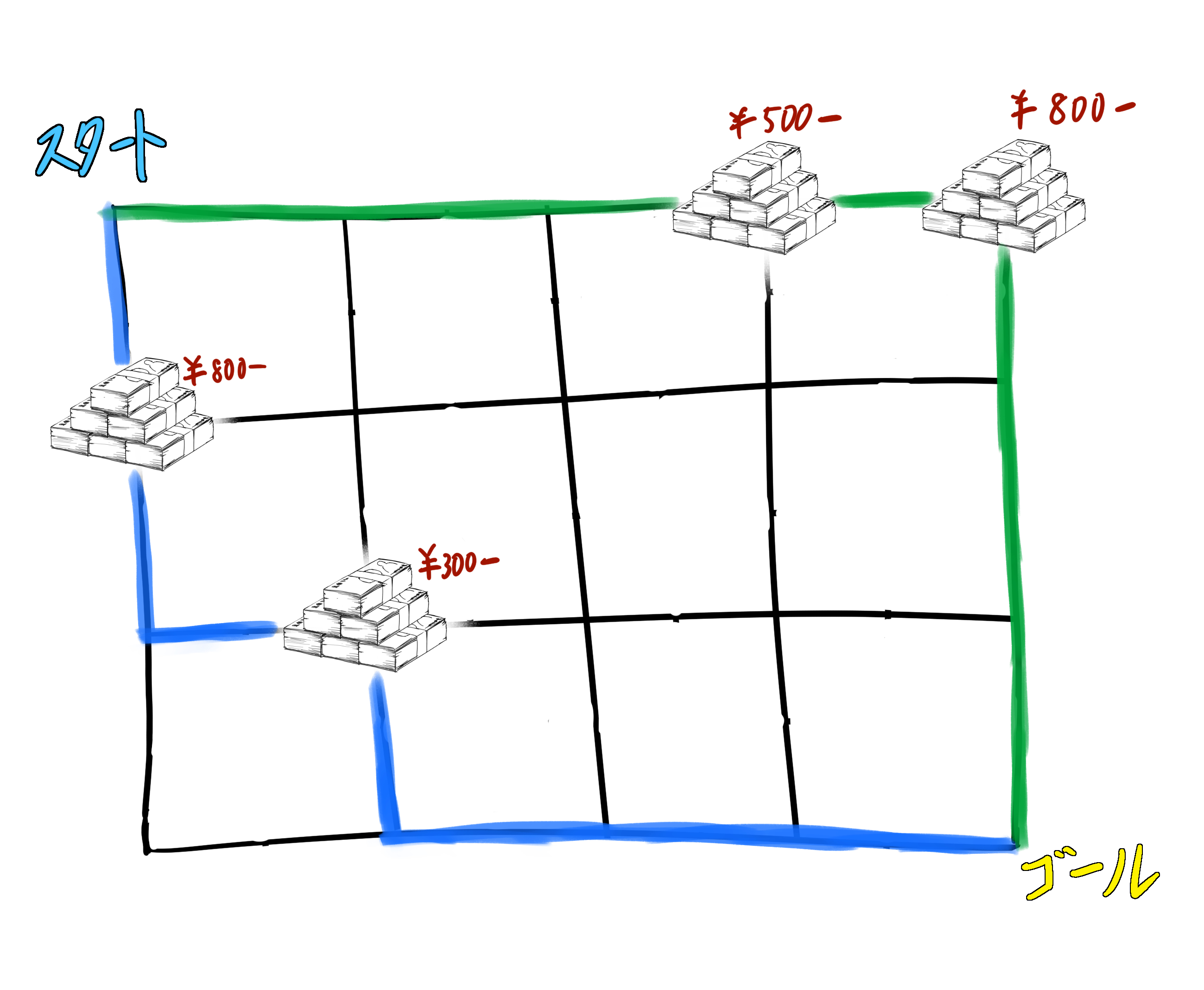
図にすると上のようになる。
最短経路は緑や青のように複数考えられる。(もちろんこれ以外にも)
今回は緑のルートを通ると拾えるお金を最大化できる。
入力2
4 4 100 100 2000 200 300 1000 500 200 700 500 10 100 500 600 10 100
出力2
3100
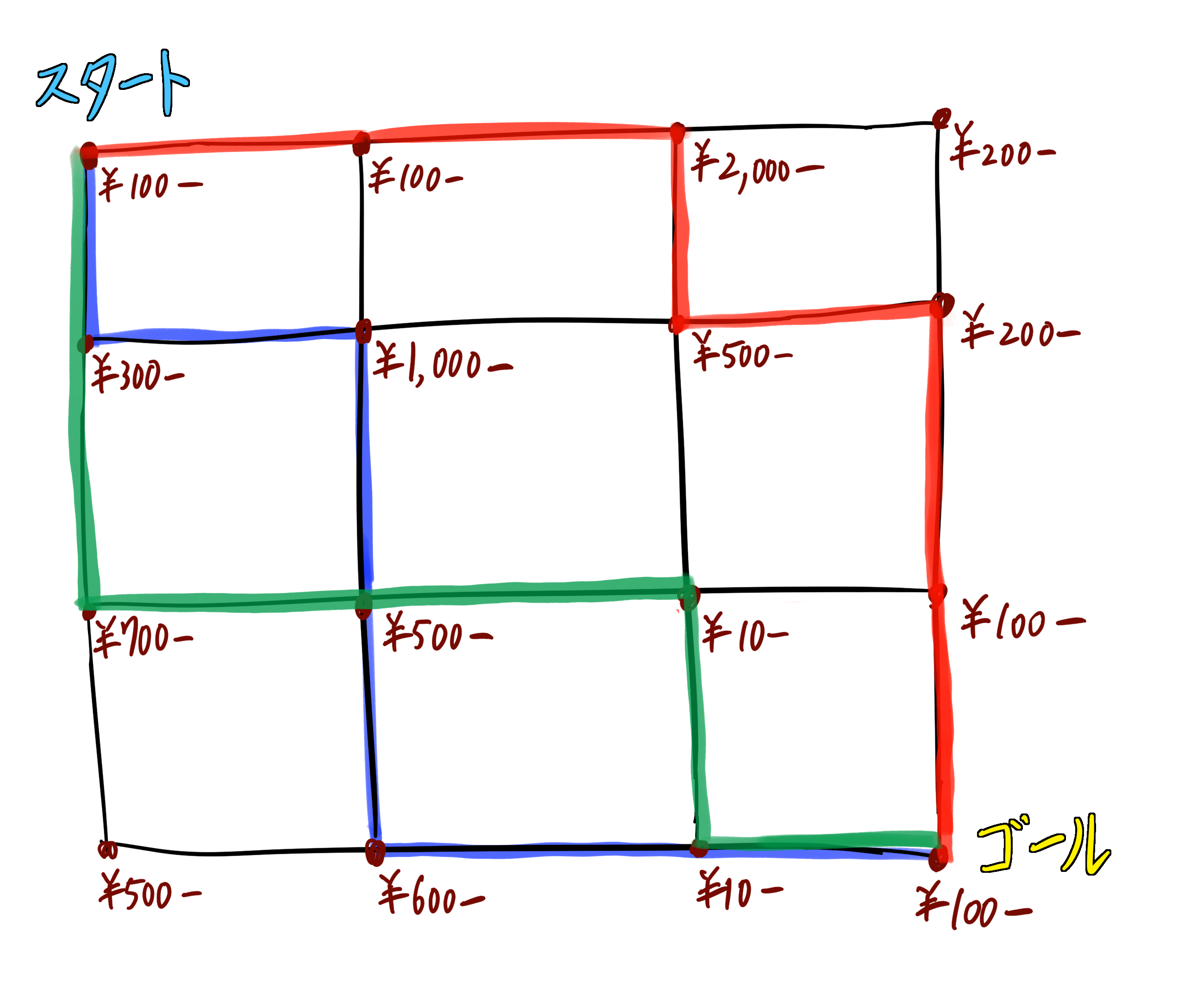
図にすると上のようになる。
この場合もやはり最短経路は赤、緑、青など複数考えられる。
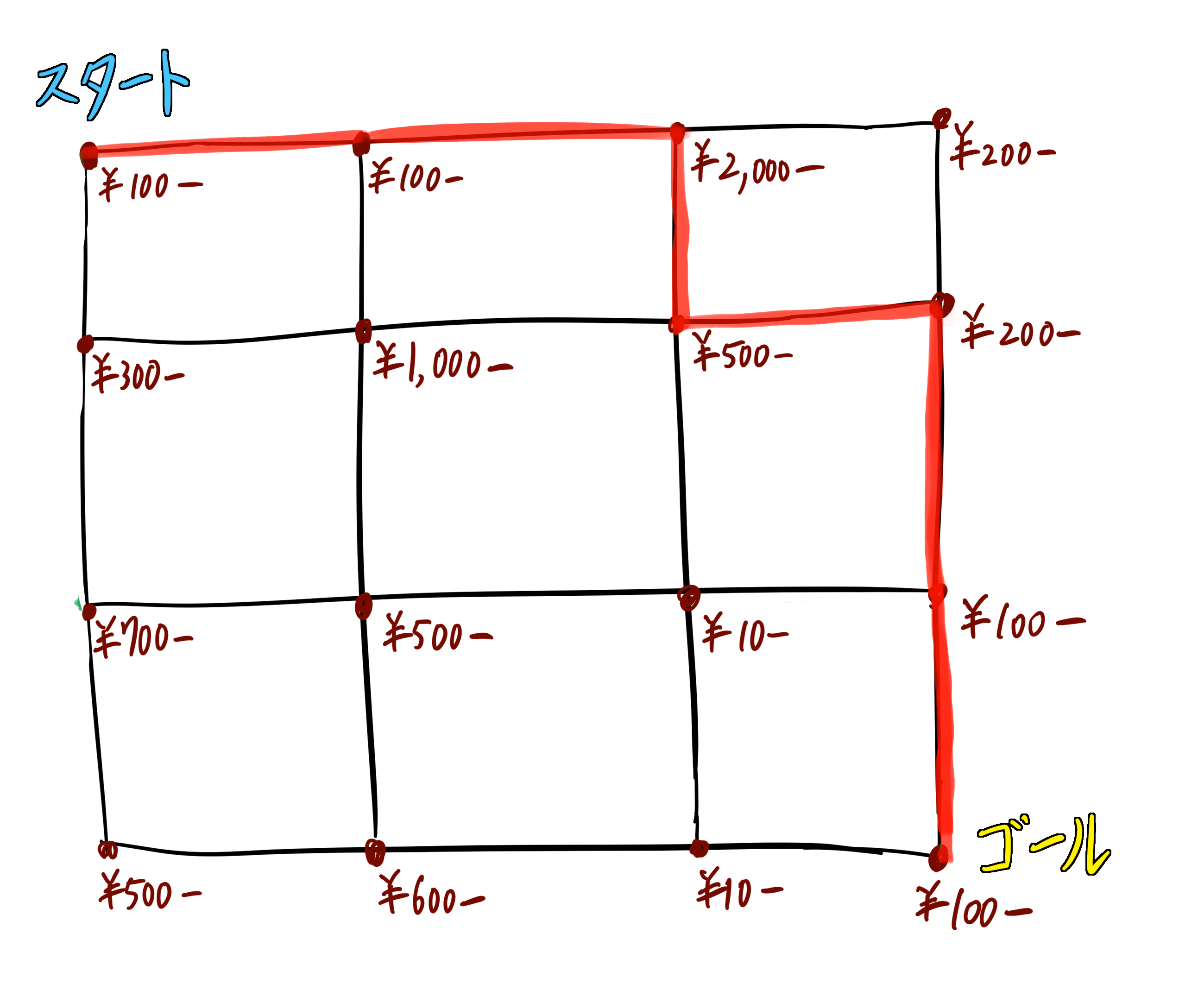
拾えるお金を最大化するルートは上図のとおりである。
解説
百円以下の拾得物は警察に届け出る必要がない。
ei1710は自分の都合のいいように解釈するので、落ちているお金を分解してとらえたり、貨幣の製造コストから考えたりしてどんなものも百円以下の拾得物にする。
ei1710は短気なので最短経路しか通らないことに注意せよ。