多重ループの練習問題だよ!! (大嘘)
問題
YDKはお宝の発掘をすることにした!
お宝は縦 H , 横 W の矩形のフィールドの地中に埋められており、どこに宝があるのかは最先端技術のおかげで事前に把握できている。
宝には価値 py,x があり、これも文明の発達のおかげで価値の大きさは事前に把握済みである。
これは、このマップにおいて上から y, 左から x の地点のお宝の価値が py,x ということである。
発掘にあたっての現地の条例として,一人当たりの発掘できる面積 S には限度があり、1つの長方形の形にしか発掘できないことになっている。
そこで、YDKは限られた面積の中で,最大でどれだけの価値のお宝を手に入れられるかを調べることにした。
入力
H W S p1,1 p1,2 ... p1,W p2,1 p2,2 ... p2,W . . pH,1 pH,2 ... pH,W
1行目にお宝が眠っているフィールドの縦の長さ H, 幅 W と発掘できる面積 S が与えられる。
続く2行目から H + 1 行目まで,お宝の価値 py,x が与えられる。
ちなみに価値が0の場合は,何も埋まっていないことを示す。
出力
指定された面積以内の長方形の区画で発掘できるお宝の、価値の総和の最大値を出力せよ。改行を忘れないこと。
発掘領域は分割してはならない。
制約
すべての入力について以下の条件を満たす。
- 1 ≤ H, W ≤ 1000
- 1 ≤ S ≤ 100
- 1 ≤ py,x ≤ 1000
入出力サンプル
入力例1
4 4 4 2 0 5 0 0 9 0 3 0 0 7 0 0 3 0 0
出力例1
16
面積 S が4以内の長方形の,縦と横の長さの組み合わせは以下のパターンがある。
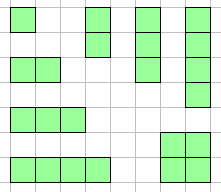
このうち 2×2 の矩形で以下の場所で発掘すると価値の総和は 9+0+0+7 = 16 となり, これが最大である。
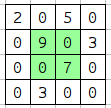
入力例2
2 3 7 9 3 0 4 2 1
出力例2
19
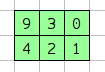
2×3 は面積 7 以内に収まっている。
その矩形内の総和 9+3+0+4+2+1 = 19 が最大である。
入力例3
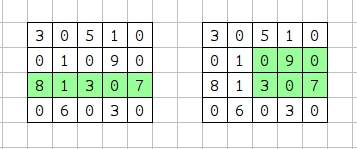
4 5 6 3 0 5 1 0 0 1 0 9 0 8 1 3 0 7 0 6 0 3 0
出力例3
19
この場合最大の価値は 19 となり、以下のように2つのパターンがある。