010 - 蜘蛛の巣上の最短経路探索
時間制限 1 秒 / メモリ制限 256 MB / 得点 10 / x 0 /
問題
PCK君は夏休みの自由研究のために、飯森山に生息するミニグモを観察しています。ミニグモの巣は図(a)に示すように、中心から放射状に均等に並んだ
$N$
本の線分と、これらの線分の上に頂点を持つ
$M$
個の同心の正
$N$
角形の枠から構成されています。同心多角形と、そのひとつ外側にある同心多角形との間の、放射状の線分に沿って測った間隔は1 cmです。同心多角形の中心から、一番内側の同心多角形の頂点までの距離も1 cmですが、この間に線分は存在しません。図は
$N$
= 8,
$M$
= 4の巣を表しています。同心多角形には中心に近い順に1から
$M$
までの番号
$i$
、放射状の各線分には0から
$N$
- 1までの番号
$j$
が割り振られており、同心多角形
$i$
と放射状の線分
$j$
の交点の座標を(
$i$
,
$j$
)で表します。
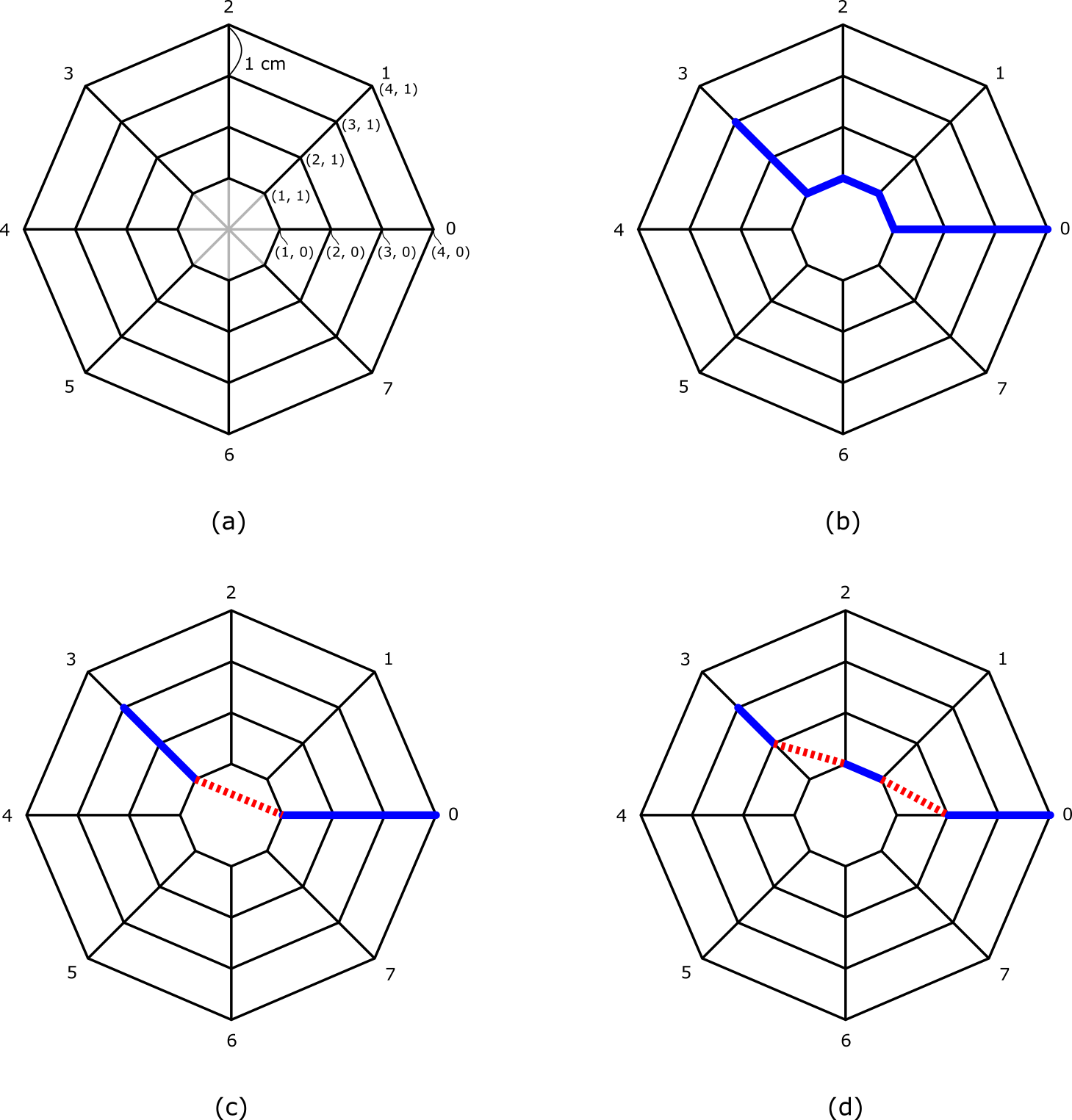
ミニグモは、巣を構成する線分を伝って交点間を移動することができ、獲物が巣にひっかかると、現在地の交点から目的地の交点まで、最短の移動距離で移動します。たとえば、図(b)は現在地(3, 3)から目的地(4, 0)への移動経路を表しています。
研究の結果、PCK君はミニグモの特殊な能力を発見しました。ミニグモは現在地から目的地まで移動する間に、巣を構成する線分に交差しない新たな線分(上図では点線で示されている)を最大
$K$
本まで生成することができるのです。たとえば、図(c)は交点(1, 3)から交点(1, 0)へ1本の新たな線分を張った、現在地(3, 3)から目的地(4, 0)への移動経路を表します。また、図(d)は交点(2, 3)から交点(1, 2)へ張った新たな線分と、交点(1, 1)から交点(2, 0)へ張った新たな線分を含む、現在地(3, 3)から目的地(4, 0)への移動経路を表します。
巣の大きさを表す情報、ミニグモの現在地と目的地、新たな線分を生成できる最大の回数が与えられる。ミニグモが現在地から目的地へ移動するための最短の距離(cm)を求めるプログラムを作成せよ。
入力
入力は以下の形式で与えられる。
$N$ $M$ $K$ $r_s$ $p_s$ $r_g$ $p_g$
1行目に放射状の線分の数 $N$ ( 4 ≤ $N$ ≤ 20 )、多角形の数 $M$ ( 2 ≤ $M$ ≤ 20 )、新たな線分を生成できる回数 $K$ ( 0 ≤ $K$ ≤ 10 )が与えられる。2行目にミニグモの現在地の座標( $r_s$ , $p_s$ )を表す2つの整数 $r_s$ , $p_s$ ( 1 ≤ $r_s$ ≤ $M$ かつ 0 ≤ $p_s$ < $N$ )が与えられる。3行目にミニグモの目的地の座標( $r_g$ , $p_g$ )を表す2つの整数 $r_g$ , $p_g$ ( 1 ≤ $r_g$ ≤ $M$ かつ 0 ≤ $p_g$ < $N$ )が与えられる。現在地の座標と目的地の座標は異なる( $r_s$ ≠ $r_g$ または $p_s$ ≠ $p_g$ )。
出力
最短の距離を1行に実数で出力する。ただし、誤差がプラスマイナス0.00001を超えてはならない。
入出力例
入力例1
8 4 0 3 3 4 0
出力例1
7.29610059
入力例2
8 4 1 3 3 4 0
出力例2
6.84775907
入力例3
8 4 2 3 3 4 0
出力例3
6.71261838