009 - だんごむしではないむし

だんごむしのような見た目の虫が平面上を歩いている．平面には直交座標が設定されており，x 軸は西から東に，y 軸は南から北に向いている．

いま，虫はある格子点 (x 座標と y 座標がともに整数である点) にいて，x 軸の正の向きを向いている．平面上のいくつかの格子点には障害物がある．虫は障害物を避けながら以下のルールで移動し続ける．

• 虫は現在の場所から，向いている方向の隣接する格子点に移動しようと試みる．
• その格子点に障害物がなければ，虫は向きを変えずにその格子点に進む．
• その格子点に障害物があれば，虫は位置を変えずに左方向に 90 度回転する．

虫の初期位置，障害物の配置，および虫の移動距離が与えられる．虫が与えられた距離だけ移動したときにいることになる位置を求めよ．

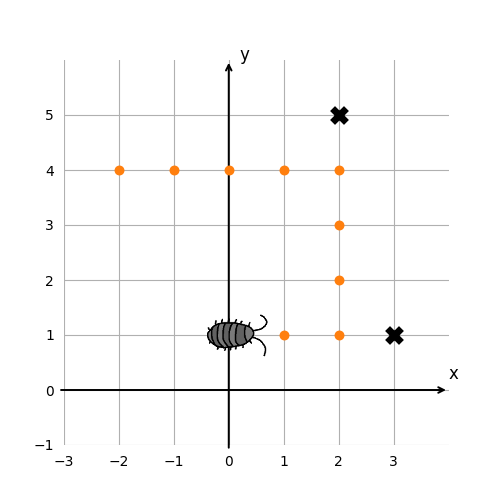
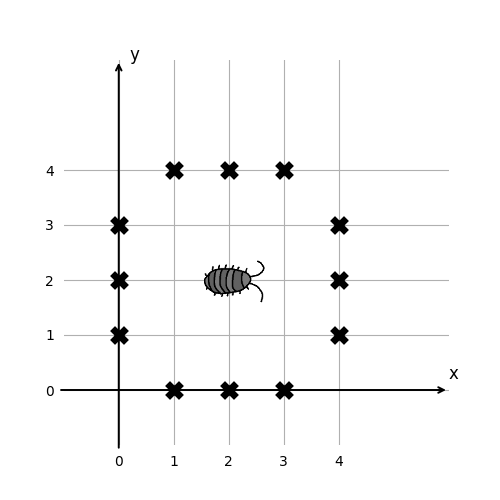
以下に Sample Input のいくつかのデータセットを図示する．バツ印で表している点が障害物のある点である．左図は最初の 2 つのデータセットである．これらのデータセットでは虫の初期位置は (0, 1) であり，(1, 1)，(2, 1) へと移動していく．次に (3, 1) へ移動しようとするが，そこには障害物があるため，向きを y 軸の正の向きに変え，(2, 2) へと移動する．虫がたどる点を橙色の丸で表している．右図はさらに次の 2 つのデータセットを示す．

入力は複数のデータセットからなる．データセットの個数は 200 を超えない．各データセットは次の形式で表される．

n
a b d
x₁ y₁
⋮
x_n y_n

ここで n は障害物の個数を表す整数である (1 ≤ n ≤ 1000)．a と b はともに 0 以上 100 以下の整数であり，虫の初期位置は座標 (a, b) である．d は移動距離を表す整数である (1 ≤ d ≤ 10¹⁸)．

i 番目の障害物は座標 (x_i, y_i) に存在する (i = 1, ⋯, n)．x_i と y_i は 0 以上 100 以下の整数である．どの 2 つの障害物の位置も異なる．すなわち，i ≠ j ならば (x_i, y_i) ≠ (x_j, y_j) である．また，どの障害物の位置も虫の初期位置 (a, b) とは一致しない．与えられた配置の下で，虫は必ず距離 d 以上移動できることが保証される．

入力の終わりは，ゼロ 1 つだけからなる行で表される．

各データセットについて，虫が距離 d だけ移動した後の位置の x, y 座標を表す 2 つの整数をスペース区切りで 1 行に出力せよ．

虫の位置の x, y 座標は負になり得ることに注意せよ．

2
0 1 4
3 1
2 5
2
0 1 9
3 1
2 5
12
2 2 11
0 1
0 2
0 3
4 1
4 2
4 3
3 4
2 4
1 4
3 0
2 0
1 0
12
2 2 7791772263873
0 1
0 2
0 3
4 1
4 2
4 3
3 4
2 4
1 4
3 0
2 0
1 0
3
0 3 198
99 2
100 3
99 4
3
0 3 1000000000000000000
99 2
100 3
99 4
1
99 100 1
100 100
0

2 3
-2 4
2 3
3 2
0 3
-999999999999999802 3
99 101