問題
平面上に無限個のマスがあります。整数の2つ組($x,y$)すべてに対して対応するマスがひとつ存在し、マス($x,y$)と呼ぶことにします。
すべてのマスは、それぞれ空きマスか壁マスのどちらか一方です。
長さ$N$の正整数列$U$ = $(U_1,U_2,...,U_N$)が与えられます。ここで、$i$ = $1,2,...,N$について$U_i$は$1 \leq U_i \leq 10^{18}$を満たします。
マス($x,y$)($1 \leq x \leq N,0 \leq y \leq U_x$)はすべて空きマスで、それ以外のマスは壁マスです。
K君が空きマスであるマス($x,y$)にいるとき、次の行動のいずれかを行うことができます。
・マス ($x+1,y$) が空きマスならば、マス ($x+1,y$) に移動する。
・マス ($x−1,y$) が空きマスならば、マス ($x−1,y$) に移動する。
・マス ($x,y+1$) が空きマスならば、マス ($x,y+1$) に移動する。
・マス ($x,y−1$) が空きマスならば、マス ($x,y−1$) に移動する。
どの空きマスどうしも、K君が行動を繰り返すことで行き来できることが保証されます。
次の形式の$Q$個のクエリを処理してください。
クエリ1
整数の4つ組($S_x,S_y,G_x,G_y$)が与えられるので、K君がマス($S_x,S_y$)にいるところからマス($G_x,G_y$)に移動するために必要な行動回数の最小値を求めてください。ただし、マス($S_x,S_y$)とマス($G_x,G_y$)は空きマスであることが保証されます。
制約:$1 \leq S_x,G_x \leq N$
クエリ2
整数の2つ組($x,y$)が与えられるので、マス($x,i$)($0 \leq i \leq y$)を空きマスに、
マス($x,j$)($y < j$)を壁マスに変更する
制約:$1 \leq x \leq N,1 \leq y \leq 10^{18}$
入力
入力は以下の形式で標準入力から与えられる。
$N$ $U_1$ $U_2$ ... $U_N$ $Q$ $query_1$ $query_2$ : $query_Q$
クエリは以下の形式で与えられる。
クエリ1
$1$ $S_x$ $S_y$ $G_x$ $G_y$
クエリ2
$2$ $x$ $y$
出力
クエリ1の回答を改行区切りで出力してください。
出力の最後に改行を入れること。
制約
全ての入出力ケースについて以下を満たす。
- $0 \leq Q,N \leq 10^{5}$
入出力例
入力例1
5 2 4 1 2 3 3 1 1 2 5 3 2 3 5 1 2 3 4 2
出力例1
7 3
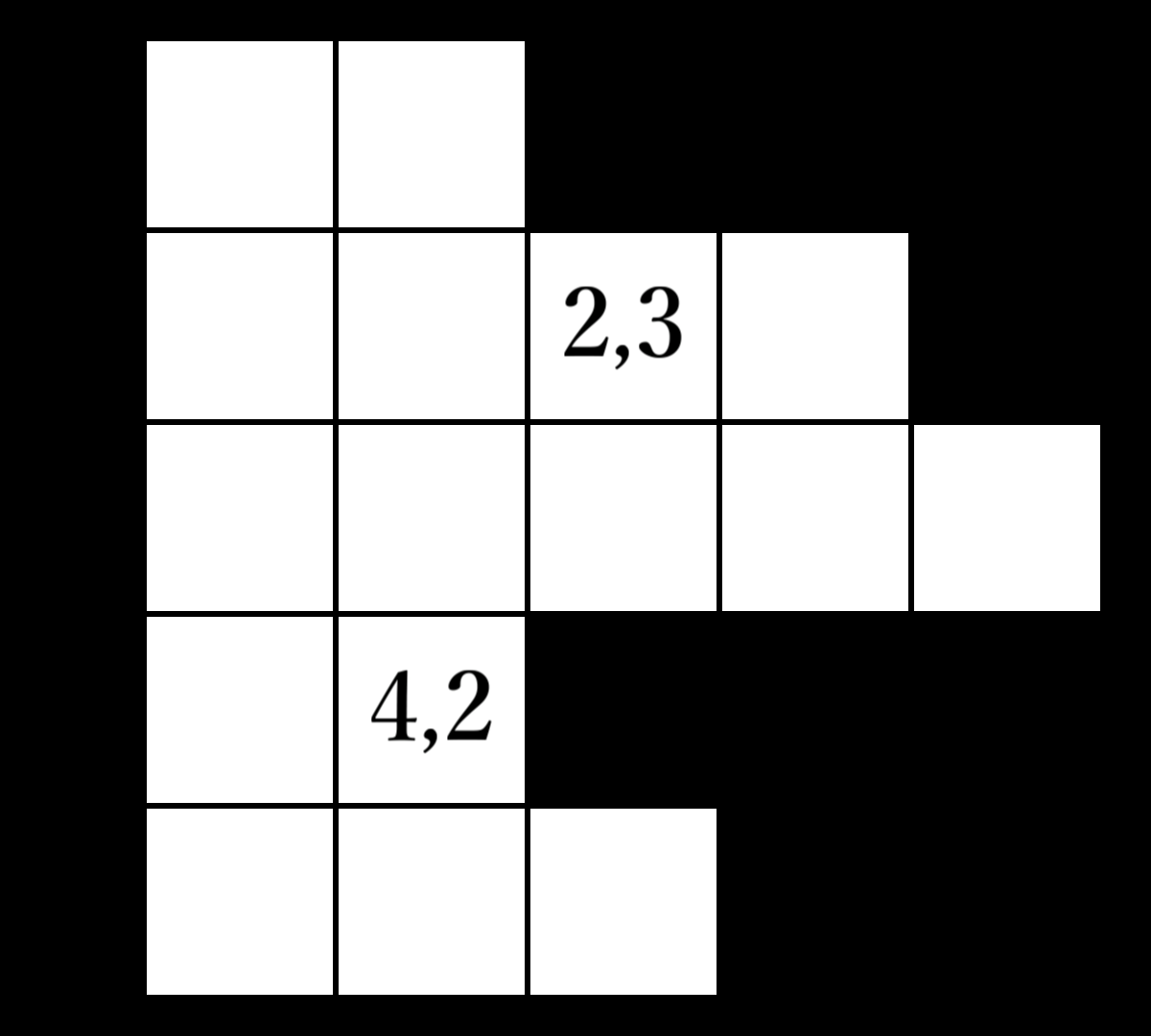
2つ目のクエリ前後でのマスの状態は以下の通りです。
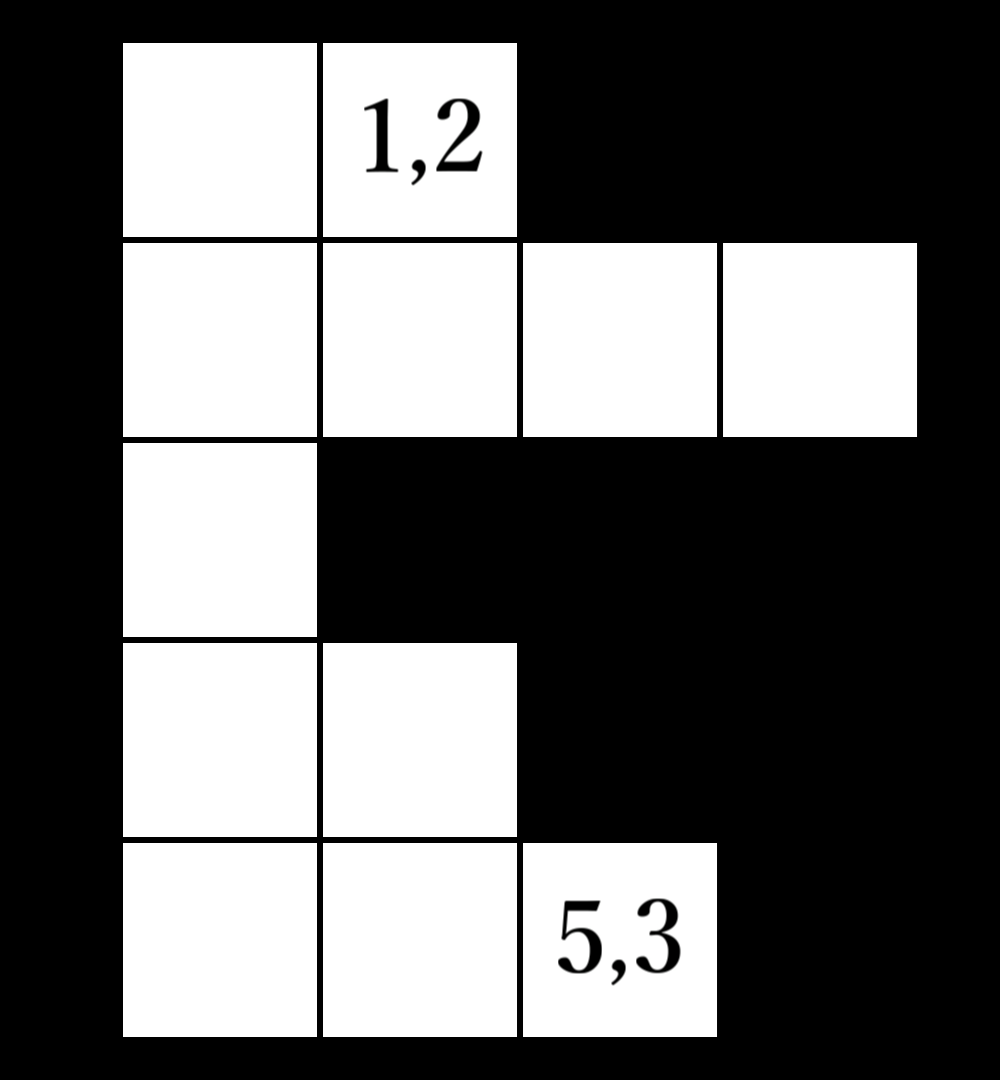
1つ目のクエリでは、マス(1,2)からマス(5,3)への距離を聞かれています。
空きマスのみを移動しなければいけないため、答えは7です。
2つ目のクエリでは、3行目の左から5マス目までを空きマスにしています。
結果、マスは右図のようになります。
入力例2
3 10 1 10 4 1 1 10 1 10 1 1 10 3 10 2 2 20 1 1 10 3 10
出力例2
0 20 2