009 - 倉庫番ロボット
時間制限 1 秒 / メモリ制限 256 MB / 得点 10 / x 1 /
問題文
アイヅ運送では倉庫番ロボットを開発しています。アイヅ運送の倉庫では、以下の平面図のように倉庫内の地点を座標$(x,y)$によって管理しています。倉庫内には、荷物が管理しやすいように、底面が正方形の棚を規則的に配置しています。倉庫内の地点の座標のペアで棚の南西隅と北東隅の位置を表すと、棚は$(0,0)$と$(1,1)$、$(2,0)$と$(3,1)$、$\cdots$、$(0,2)$と$(1,3)$、$(2,2)$と$(3,3)$、$\cdots$、というように、倉庫の端から端まで、$0$以上の整数$i$と$j$を使って$(2i,2j)$と$(2i+1,2j+1)$で表される正方形の領域を占めるように置かれています。
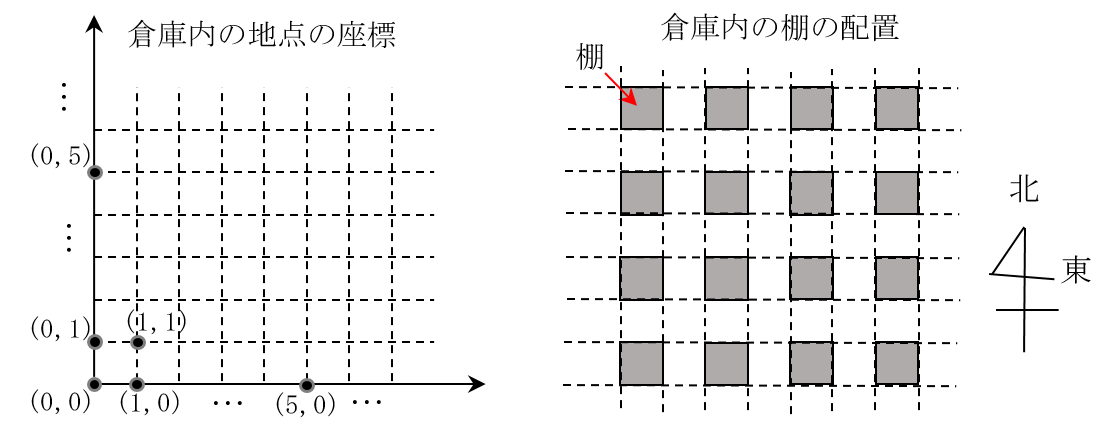
倉庫番ロボットは、棚のないところでは自由に動くことができます。棚が置かれている領域内を通り抜けることはできませんが、サイズが小さいので棚の領域の境界上を通ることはできます。例えば、地点$(0,0)$から地点$(4,3)$へ最短距離で向かうには、以下のように動くことができます。
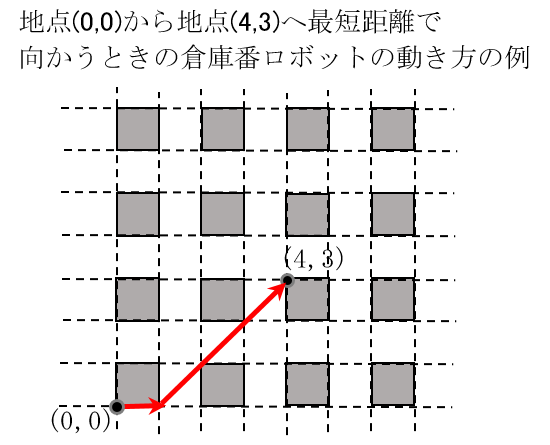
倉庫番ロボット開発部のあなたは、ロボットに目標地点までの最短距離を計算する機能を付けようと考えています。
課題
倉庫番ロボットが現在いる地点と、目標の地点が与えられたとき、ロボットが目標の地点に到達するために移動する最短距離を出力するプログラムを作成せよ。
入力
入力は以下の形式で与えられる。
$x_{0} \ y_{0} \ x_{1} \ y_{1}$
1行に倉庫番ロボットが現在いる地点の座標$x_{0},y_{0}\ (0 \leq x_{0},y_{0} \leq 300)$と、目標の地点の座標$x_{1},y_{1}\ (0 \leq x_{1},y_{1} \leq 300)$が、すべて整数で与えられる。
倉庫は与えられる座標の地点がすべて存在するような大きさの長方形であると考えてよい。ロボットが現在いる地点と目標の地点の座標は異なる $(x_{0} \neq x_{1}$ または $y_{0} \neq y_{1})$ 。
出力
ロボットが目標の地点に到達するための最短距離を、$1$行に実数で出力する。
ただし、誤差がプラスマイナス $0.00001$ を超えてはならない。
入出力例
入力例1
0 0 4 3
出力例1
5.24264069
入力例2
7 1 1 6
出力例2
7.89292223
入力例3
0 2 5 2
出力例3
5